This post is mostly for intuitive understanding of Word2Vec model, one can refer to sufficient details in the CS224N course notes where it goes through Cross-entropy, CBOW, Skip-gram and Negative Sampling in order.

How to form the training set?

Denote the training set as \(D\). For each sentence in our corpus, we set each word in the sentence as the center word. Then, given a context window of size \(C\), we select the left and right context words up to \(C\) steps from the center word, e.g. for \(C = 2\), we have:

{...} - center word
[...] - window context
C = 2

the [skip-gram model {predicts} context words] given the target word and CBOW does the reverse.

D = {...,
(predict, skip-gram),  
(predict, model),
(predict, context),
(predict, word),
...
}

The training set is formed by the (center, context) pairs. Mathematically, for \(i\)th sentence of length \(L_i\),

\[D_i = \{ (w_t, w_c) \vert 1 \leq t \leq L_i; \lvert c - t \rvert \leq C ; 1 \leq c \leq L_i \}\]

where \(w_t\) and \(w_c\) are the center word and the context word, respectively. Thus, \(D = \bigcup_i D_i\).

Note: The stop words could be removed from the training set during preprocessing. The third condition in the above expression is to bound the context window within the sentence.

Skip-gram

The objective is to maximise the conditional probability of the [context words given the center word] [for all the center words] (two loops):

\[\max \prod_{t} \prod_{c} P(\text{context}_c | \text{center}_t; \theta) = \prod_{1 \leq t \leq T} \prod_{-C \leq j \leq C, j \neq 0} P(w_{t+j} | w_t; \theta)\]

where \(T\) is the total This is equivalent to minimize the negative log probability as for batch gradient descent:

\[J(\theta) = - \frac{1}{T} \sum_{1 \leq t \leq T} \sum_{-C \leq j \leq C, j \neq 0} \log P(w_{t+j} | w_t; \theta)\]

Note: This is not a perfect expression because it does not consider the gaps among sentences and the lengths of the sentences. Note: The objective function actually comes from teh Cross-entropy Loss in the NLP case (with each word as a single class).

The skip-gram architecture is simply a 2-layer neural network (input-hidden-softmax) with two weight matrices \(W_{input}\) and \(W_{output}\), both of which have the shape \(\lvert V \rvert \times N\) where \(N\) is the hidden (embedding) size. Thus, the parameter involved in the cost function is the concatenation of the two matrices, i.e. \(\theta = [W_{input} W_{output}] \in \mathbb{R}^{2VN}\). The row vectors (with shape \(1 \times N\)) of \(W_{input}\) (resp. \(W_{output}\)) are word vectors for input center words (resp. output context words).

Forward propagation (see the example figure below)

  1. The input is the one-hot encoding vector \(x\) for the current center word, and the corresponding word vector can be obtained by \(h = W_{input}^T x\) (with shape \(N \times 1\)).
  2. The output matrix \(W_{output}\) are word vectors for context words, so \(W_{output} h\) will return the similarity vector of shape \(\lvert V \rvert \times 1\) with the \(i\)th cell storing a similarity score between the input center word and the \(i\)th word in the vocabulary.
  3. The similarity vector is then fed into the softmax output layer, giving the probability distribution of each word being the context word of the input center word.
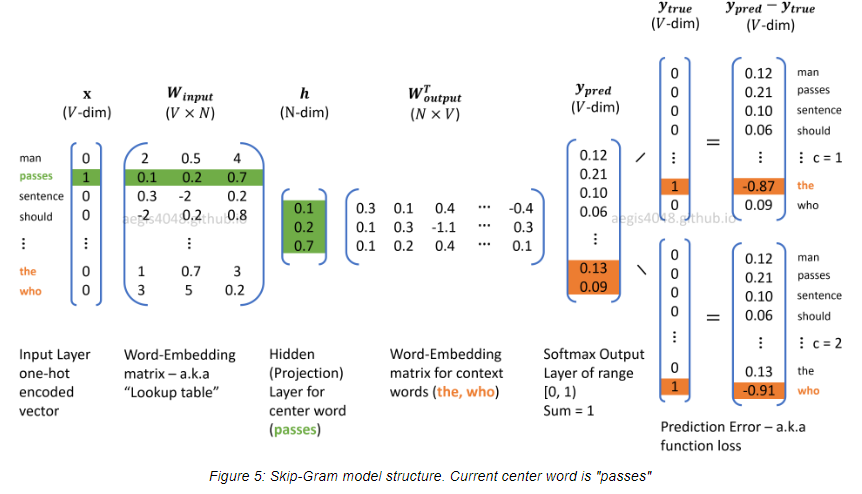
skip-gram

Fig. 1: An example figure of the skip-gram model is taken from the post here.

References